Matlab Tutorial - Introduction to FFT & DFT

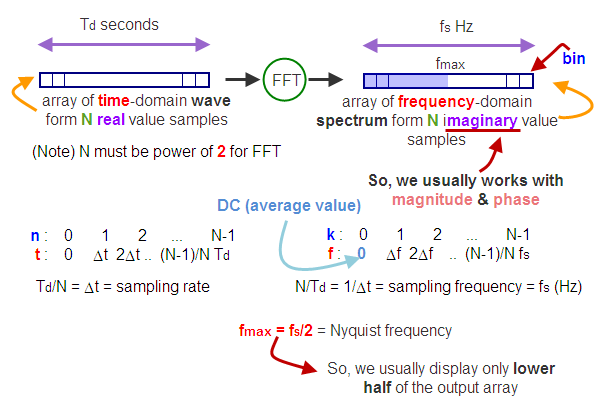
A Fast Fourier transform (FFT) is a fast computational algorithm to compute the discrete Fourier transform (DFT) and its inverse. The Fast Fourier Transform does not refer to a new or different type of Fourier transform. It refers to a very efficient algorithm for computing the DFT.

The time takes to perform a DFT on a computer depends primarily on the number of multiplications involved ($O (N^2))$ while FFT only needs $Nlog_2(N)$.

The central insight which leads to this algorithm is the realization that a discrete Fourier transform of a sequence of $N$ points can be written in terms of two discrete Fourier transforms of length $N/2$. Therefore, if $N$ is a power of 2, it is possible to recursively apply this decomposition.

Here are the functions related to FFT and DFT. The cases actually using these functions are in other pages.

1. The function $dft()$ computes the discrete Fourier transform. Define a vector $x$ and compute the DFT using the command:

   X = dft(x)
   

   The first element in $X$ corresponds to the value of $X(0)$.
2. $idft()$ computes the inverse discrete Fourier transform. Define a vector $X$ and compute the IDFT using the command

   x = idft(X)
   

   The first element of the resulting vector $x$ is $x[0]$.
3. For a more efficient but less obvious program, the discrete Fourier transform can be computed using the function $fft()$ which performs a Fast Fourier Transform of a sequence of numbers. To compute the FFT of a sequence $x[n]$ which is stored in the vector $x$, use the command

   X = fft(x)
   

   If we use this way, the $fft()$ is interchangeable with the command $dft()$. For more computational efficiency, the length of the vector $x$ should be equal to the power of 2, that is 64, 128, 512, etc. The vector $x$ can be padded with zeros to make it have an appropriate length. MATLAB does this automatically by using the following command where $N$ is defined to be an power of 2:

   X = fft(x,N);
   

   The longer the length of $x$, the finer the grid will be for the FFT. Due to a wrap around effect, only the first $N/2$ points of the FFT have any meaning.
4. The $ifft()$ function computes the inverse Fourier transform:

   x = ifft(X);
   

5. The FFT can be used to approximate the Fourier transform of a continuous-time signal. A continuous-time signal $x(t)$ is sampled with a period of $T$ seconds, then the DFT is computed for the sampled signal. The resulting amplitude must be scaled and the corresponding frequency determined. An M-file that approximates the Fourier Transform of a sampled continuous-time signal can be downloaded from contfft.m. Let a vector $x $be defined as the sampled continuous-time signal $x(t)$ and let $T$ be the sampling time.

   [X,w] = contfft(x,T);
   

   The outputs are the Fourier transform stored in the vector $X$ and the corresponding frequency vector $w$.