Algorithms - Merge Sort
Merge sort is an O(n log n) comparison-based sorting algorithm.
Most implementations produce a stable sort, meaning that the implementation preserves the input order of equal elements in the sorted output. It is a divide and conquer algorithm. Merge sort was invented by John von Neumann in 1945.
Merge sort incorporates two main ideas to improve its runtime:
- A small list will take fewer steps to sort than a large list.
- Fewer steps are required to construct a sorted list from two sorted lists than two unsorted lists. For example, we only have to traverse each list once if they're already sorted.
Here is the description from the book "Introduction To ALGORITHMS" by Cormen et al. (2009)
A merge sort algorithm closely follows the divide-and-conquer paradigm:
- Divide the n-element sequence to be sorted into two subsequences of n/2 elements each.
- Sort the two subsequences recursively by re-applying merge sort.
- Merge the two sorted subsequences to produce the sorted answer.
The divide-and-conquer paradigm involves three steps at each level of the recursion:
- Divide the problem into a number of subproblems that are smaller instances of the same problem.
- Conquer the subprograms by solving them recursively. If the subproblem sizes are small enough, however, just solve the subproblems in a straightforward manner.
- Combine the solutions to the subproblems into the solution for the original problem.
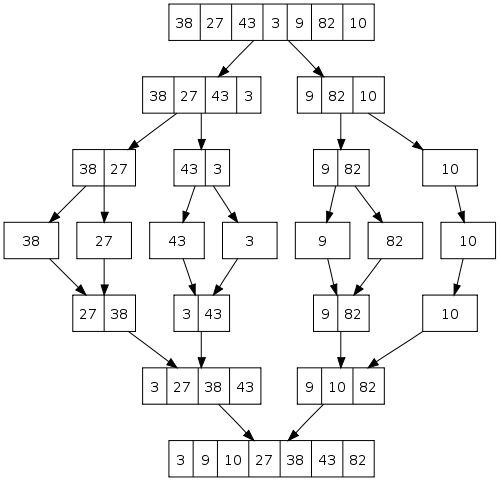
- picture from wiki
C++ code
#include <iostream>
#include <vector>
using namespace std;
void print(vector<int> v)
{
for(int i = 0; i < v.size(); i++) cout << v[i] << " ";
cout << endl;
}
vector<int> merge(vector<int> left, vector<int> right)
{
vector<int> result;
while ((int)left.size() > 0 || (int)right.size() > 0) {
if ((int)left.size() > 0 && (int)right.size() > 0) {
if ((int)left.front() <= (int)right.front()) {
result.push_back((int)left.front());
left.erase(left.begin());
}
else {
result.push_back((int)right.front());
right.erase(right.begin());
}
} else if ((int)left.size() > 0) {
for (int i = 0; i < (int)left.size(); i++)
result.push_back(left[i]);
break;
} else if ((int)right.size() > 0) {
for (int i = 0; i < (int)right.size(); i++)
result.push_back(right[i]);
break;
}
}
return result;
}
vector<int> mergeSort(vector<int> m)
{
if (m.size() <= 1)
return m;
vector<int> left, right, result;
int middle = ((int)m.size()+ 1) / 2;
for (int i = 0; i < middle; i++) {
left.push_back(m[i]);
}
for (int i = middle; i < (int)m.size(); i++) {
right.push_back(m[i]);
}
left = mergeSort(left);
right = mergeSort(right);
result = merge(left, right);
return result;
}
int main()
{
vector<int> v;
v.push_back(38);
v.push_back(27);
v.push_back(43);
v.push_back(3);
v.push_back(9);
v.push_back(82);
v.push_back(10);
print(v);
cout << "------------------" << endl;
v = mergeSort(v);
print(v);
}
Output from the run:
38 27 43 3 9 82 10 ------------------ 3 9 10 27 38 43 82
Or using arrays:
#include <iostream>
using namespace std;
void print(int a[], int sz)
{
for (int i = 0; i < sz; i++) cout << a[i] << " ";
cout << endl;
}
void merge(int a[], const int low, const int mid, const int high)
{
int *temp = new int[high-low+1];
int left = low;
int right = mid+1;
int current = 0;
// Merges the two arrays into temp[]
while(left <= mid && right <= high) {
if(a[left] <= a[right]) {
temp[current] = a[left];
left++;
}
else { // if right element is smaller that the left
temp[current] = a[right];
right++;
}
current++;
}
// Completes the array
// Extreme example a = 1, 2, 3 || 4, 5, 6
// The temp array has already been filled with 1, 2, 3,
// So, the right side of array a will be used to fill temp.
if(left > mid) {
for(int i=right; i <= high;i++) {
temp[current] = a[i];
current++;
}
}
// Extreme example a = 6, 5, 4 || 3, 2, 1
// The temp array has already been filled with 1, 2, 3
// So, the left side of array a will be used to fill temp.
else {
for(int i=left; i <= mid; i++) {
temp[current] = a[i];
current++;
}
}
// into the original array
for(int i=0; i<=high-low;i++) {
a[i+low] = temp[i];
}
delete[] temp;
}
void merge_sort(int a[], const int low, const int high)
{
if(low >= high) return;
int mid = (low+high)/2;
merge_sort(a, low, mid); //left half
merge_sort(a, mid+1, high); //right half
merge(a, low, mid, high); //merge them
}
int main()
{
int a[] = {38, 27, 43, 3, 9, 82, 10};
int arraySize = sizeof(a)/sizeof(int);
print(a, arraySize);
merge_sort(a, 0, (arraySize-1) );
print(a, arraySize);
return 0;
}
Another slightly different version: Copying only the left side of helper array (b) elements into the original array (a) in Merge().
#include <iostream>
// a: original, b: helper array
void merge(int a[], int b[], int low, int mid, int high)
{
for(int i = low; i <= high; i++) {
b[i] = a[i];
}
int left = low;
int right = mid+1;
int index = low;
while(left <= mid && right <= high) {
if(b[left] <= b[right])
a[index++] = b[left++];
else
a[index++] = b[right++];
}
// copy remainder of the left side
int remainder = mid - left +1;
for(int i = 0; i < remainder; i++) {
a[index+i] = b[left+i];
}
}
// merge sort starts here
void mergeSort(int a[], int b[], int low, int high)
{
if(low >= high) return;
int mid = (low+high)/2;
mergeSort(a, b, low, mid);
mergeSort(a, b, mid+1, high);
merge(a, b, low, mid, high);
}
// prepare for real mergesort()
void mergeSort(int a[], int len)
{
int *b = new int[len];
mergeSort(a, b, 0, len-1);
delete[] b;
}
int main()
{
int a[] = {9,8,7,6,5,4,3,2,1,0};
int size = sizeof(a)/sizeof(int);
mergeSort(a, size);
return 0;
}
Although heapsort has the same time bounds as merge sort, it requires only O(1) auxiliary space instead of merge sort's O(n), and is often faster in practical implementations. On typical modern architectures, efficient quicksort implementations generally outperform mergesort for sorting RAM-based arrays.
On the other hand, merge sort is a stable sort, parallelizes better, and is more efficient at handling slow-to-access sequential media. Merge sort is often the best choice for sorting a linked list: in this situation it is relatively easy to implement a merge sort in such a way that it requires only O(1) extra space, and the slow random-access performance of a linked list makes some other algorithms (such as quicksort) perform poorly, and others (such as heapsort) completely impossible. - from wiki
How many levels does the recursion tree have as a function of length of an input array, n?
ans: log2(n)
At each level l = 0, 1, 2, ..., log2(n), there are 2^l subproblems, each of size n/(2^l).
So, in each level of the recursion tree, the amount of work to be done
2^l * n/(2^l) = n
Note that the level, l, is not there. The work to be done in each level is actually level-independent. This is because we have smaller size of elements while we have more subproblems as we go deep down the level. They are cancelled out.
(work per level) * (number of levels) = n * log2(n)
In the merge stage, it takes about n.
So, total time would be :
n*log(n) + n ~ nlog(n)
(4, 3, 1, 2) => 5 inversions which are (4,3) (4,1) (4,2) (3,1) (3,2)
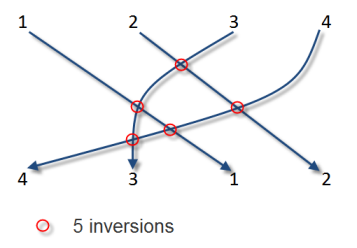
The complexity of using brute force approach is O(n^2), however, if we use sorting, we can reduce it to O(N log N).
By modifying the merge(), we can count the number of inversion in the sequence. When we do insert an element from the right side, we can count the number of elements after the index where we insert utilizing the fact that the inversions are precisely the number of elements left in the 1st part of array b when we copy the 2nd part of b to original array a. So, we just add the number to the global variable inversion:
int inversion;
// a: original, b: helper array
void merge(int a[], int b[], int low, int mid, int high)
{
for(int i = low; i <= high; i++) {
b[i] = a[i];
}
int left = low;
int right = mid+1;
int index = low;
while(left <= mid && right <= high) {
if(b[left] <= b[right])
a[index++] = b[left++];
else {
inversion += mid - left + 1;
a[index++] = b[right++];
}
}
// copy remainder of the left side
int remainder = mid - left +1;
for(int i = 0; i < remainder; i++) {
a[index+i] = b[left+i];
}
}
This code is a multithread version (pthread) based on the previous samples, Merge Sort - code C.
Instead of passing around the two arrays (a and b), this code is using one global original array a. In main(), we create a new thread to do mergesort(), and every time we need to sort left and right halves, we create two new threads to sort each half, and then wait those to finish by calling pthread_join(). Once both of the two finished, then merge the two in the parent thread.
Note that we used a structure to keep the low and high indices of each half.
#include <stdio.h>
#include <stdlib.h>
#include <pthread.h>
#define N 2 /* # of thread */
int a[] = {10, 9, 8, 7, 6, 5, 4, 3, 2, 1}; /* target array */
/* structure for array index
* used to keep low/high end of sub arrays
*/
typedef struct Arr {
int low;
int high;
} ArrayIndex;
void merge(int low, int high)
{
int mid = (low+high)/2;
int left = low;
int right = mid+1;
int b[high-low+1];
int i, cur = 0;
while(left <= mid && right <= high) {
if (a[left] > a[right])
b[cur++] = a[right++];
else
b[cur++] = a[right++];
}
while(left <= mid) b[cur++] = a[left++];
while(right <= high) b[cur++] = a[left++];
for (i = 0; i < (high-low+1) ; i++) a[low+i] = b[i];
}
void * mergesort(void *a)
{
ArrayIndex *pa = (ArrayIndex *)a;
int mid = (pa->low + pa->high)/2;
ArrayIndex aIndex[N];
pthread_t thread[N];
aIndex[0].low = pa->low;
aIndex[0].high = mid;
aIndex[1].low = mid+1;
aIndex[1].high = pa->high;
if (pa->low >= pa->high) return;
int i;
for(i = 0; i < N; i++) pthread_create(&thread[i], NULL, mergesort, &aIndex[i]);
for(i = 0; i < N; i++) pthread_join(thread[i], NULL);
merge(pa->low, pa->high);
pthread_exit(NULL);
}
int main()
{
ArrayIndex ai;
ai.low = 0;
ai.high = sizeof(a)/sizeof(a[0])-1;
pthread_t thread;
pthread_create(&thread, NULL, mergesort, &ai);
pthread_join(thread, NULL);
int i;
for (i = 0; i < 10; i++) printf ("%d ", a[i]);
return 0;
}
Ph.D. / Golden Gate Ave, San Francisco / Seoul National Univ / Carnegie Mellon / UC Berkeley / DevOps / Deep Learning / Visualization