tf-idf
"In a large text corpus, some words will be very present (e.g. "the", "a", "is" in English) hence carrying very little meaningful information about the actual contents of the document. If we were to feed the direct count data directly to a classifier those very frequent terms would shadow the frequencies of rarer yet more interesting terms." - from sklearn.feature_extraction : tf-idf term weighting.
The tf-idf (term frequency-inverse document frequency) is used to weigh how important a word of a document in a document collection. It is often used as a weighting factor in information retrieval and data mining. So, tf-idf weight for a term is the product of its tf weight and idf weight. It's the best known weighting scheme in information retrieval. Sometime people denote it as tf.idf.
The tf-idf increases not only with the number of occurrences in a document but also with the rarity of the term in the collection (see also Shannon Entropy).
$$tf \text- idf(t,d,D) = tf(t,d) \times idf(t,D)$$where
$$tf(t,d) = f(t,d)$$ $$idf(t,d) = log { N \over | \{ d \in D : t \in d \} | } $$A raw frequency ($f(t,d)$) is the number of times that term $t$ occurs in a document. We'll use this raw frequency for term frequency ($tf(t,d)$).
$N$ is the total number of documents in the collection, and $\left|\{d \in D: t \in d\}\right|$ is the number of documents where the term $t$ appears.
We have term frequency tables for a collection consisting of only two documents as shown below.
- Document 1: "It was many and many a year ago nn a kingdom by the sea"
- Document 2: "I was a child and she was a child in this kingdom by the sea"
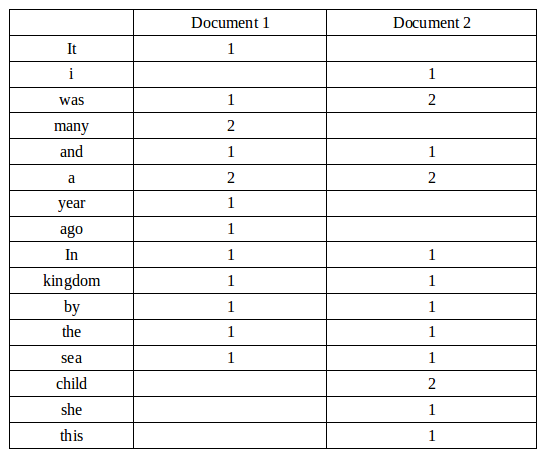
We want to calculate tf-idf for the term "kingdom" in document 1, and it is performed as follows:
tf is simply the frequency that we look up in appropriate table. In our case, it's one. However, idf is not that straight forward:
$$idf(kingdom,d) = log { N \over | \{ d \in D : t \in d \} | } $$The numerator is the number of documents, which is two. The number of documents in which "kingdom" appears is also two. So, it gives us:
$$idf(kingdom,d) = log { 2 \over 2 } = 0 $$As a result, tf-idf is zero for the term, "kingdom".
We get a slightly more outcome from the word "child", which occurs two times but in only one document. For this document #2, tf-idf of "child"" is:
$$tf(child, d_2) = 2 $$ $$idf(child, D) = log {2 \over 1} = 0.3010$$ $$tf \text-idf(child, d_2, D) = tf(child, d_2) \times idf(child, D) = 2 \times log 2 \approx 0.6$$Ph.D. / Golden Gate Ave, San Francisco / Seoul National Univ / Carnegie Mellon / UC Berkeley / DevOps / Deep Learning / Visualization